C++

C++ – 最小生成树

_Redstone_c_

定义

  1. 连通图：任意两个顶点vi与vj都有路径相通。
  2. 强连通图：任意两个顶点vi与vj都有路径相通。
  3. 连通图：图的边具有一定的意义，每一条变都有对应着一个权。
  4. 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点。
  5. 最小生成树：建立生成树且所花费的权最少。

PS：如果生成树中再添加一条边，则必定成环。

最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

贪心算法：

每一步都要最好的，权重最小的边。

需要的约束：

  1. 智能用图里有的边。
  2. 智能正好用掉|v|-1条边。
  3. 不能有回路。

Kruskal 算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

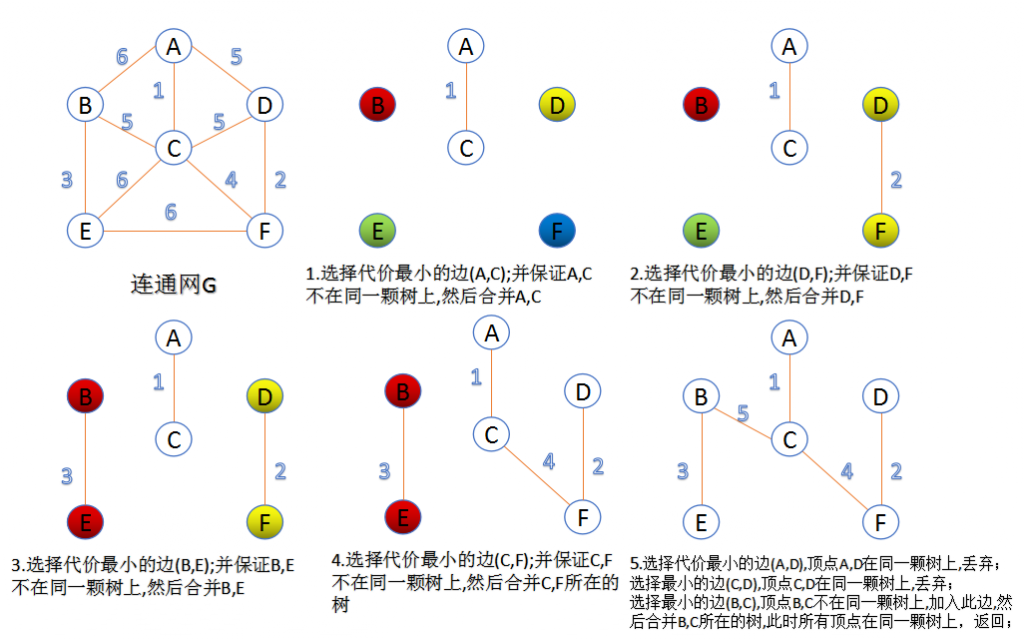
  1. 把图中的所有边按代价从小到大排序。
  2. 把图中的n个顶点看成独立的n棵树组成的森林。
  3. 按权值从小到大选择边，所选的边连接的两个顶点ui，vi，应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一棵树。
  4. 重复[3]，直到所有顶点都在一棵树内或者有n-1条边为止 。

伪代码

void Kruskal(Graph G) {
    MST = {};
    while(MST中不到|V|-1条边&&E中还有边) {
        从E中取一条权重最小的边E(V,W);
        将E(V,W)从E中删除;
        if(E(V,W)不在MST中构成回路)
            将E(V,W)加入MST;
        else
            彻底无视E(V,W);
    }
    if(MST中不到|V|-1条边)
        Error(生成树不存在);
}

T = O(|E|log|E|)

完全代码

int ans;
int fat[MAXN];
int tfind(int n) {
    if(fat[n] != n) fat[n] = tfind(fat[n]);
    return fat[n];
}
void kruskal() {
    ans = 0;
    sort(edge, edge + tot);
    for(int i = 0; i < n; i++) fat[i] = i;
    for(int i = 0; i < tot; i++) {
        if(tfind(edge[i].u) != tfind(edge[i].v)) {
            ans += edge[i].w;
            fat[tfind(edge[i].u)] = tfind(edge[i].v);
        }
    }
}

Prim 算法

此算法可以称为”加点法“，每次迭代选择代价最小的边对应的点，加入到最小生成树中。

算法从某一顶点s开始，逐渐长达覆盖整个连通网的所有顶点。

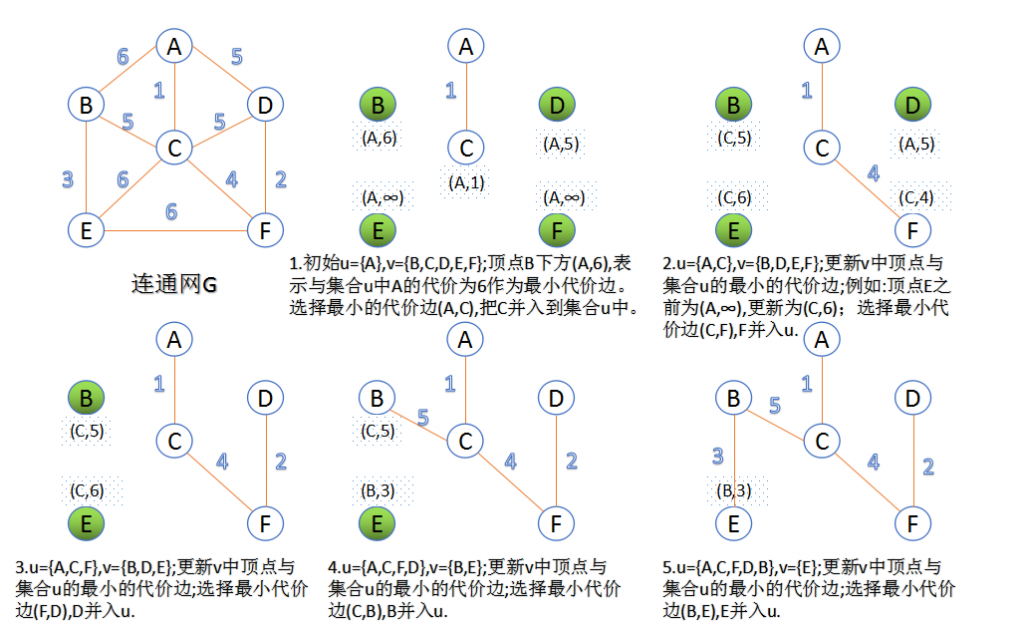
  1. 图的所有顶点集合为V；初始令集合u={s},v=V−u。
  2. 在两个集合u，v能过够组成的边中，选择一条代价最小的边（u0，v0），加入到最小生成树中，并把v0并入到集合u中。
  3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

伪代码

void Prim() {
    MST = {s};
    while(true) {
        V = 未收录顶点中dist最小者;
        if(这样的V不存在)
            break;
        将V收录进MST：dist[V] = 0;
        for(V的每个邻接点W)
            if(dist[W]!=0)
                if(E(v,w) < dist[W]) {
                    dist[W] = E(v,w);
                    parent[W] = V;
                }
    }
    if(MST中收的顶点不到|V|个)
        Error(生成树不存在);
}

T=O(|V|2)

完全代码

int ans;
bool vis[MAXN];
int dis[MAXN];
void prim() {
    memset(vis, false, sizeof vis);
    memset(dis, INF, sizeof dis);
    for(int i = head[0]; ~i; i = edge[i].nxt)
        if(dis[edge[i].v] > edge[i].w)
            dis[edge[i].v] = edge[i].w;\
    vis[0] = true;
    ans = 0;
    while(true) {
        int k = 0;
        int minn = INF;
        for(int i = 0; i < n; i++) {
            if(!vis[i] && dis[i] < minn) {
                minn = dis[i];
                k = i;
            }
        }
        if(minn == INF) return;
        vis[k] = true;
        ans += dis[k];
        dis[k] = 0;
        for(int i = head[k]; ~i; i = edge[i].nxt)
            if(!vis[edge[i].v] && dis[edge[i].v] > edge[i].w)
                dis[edge[i].v] = edge[i].w;
    }
}

发表回复